Discontinuous Analysis
Analysis of any functions, not only continuous ones
9 followers
Analysis of any functions, not only continuous ones
9 followers
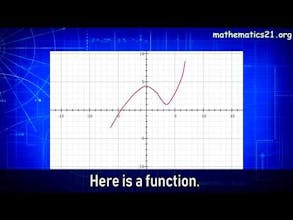
Discontinuous Analysis is a novel way of calculus of any functions, not only differentiable or continuous. It is based on "generalized limit" that is defined for every function at all points. This helps to skip existence check during calculations + QG research